voriges Kapitel | nächstes Kapitel
Eine höhere Form der Verschlüsselung stellen die polyalphabetischen Substitutionschiffren dar, die, wie der Name bereits andeutet, mehrere Geheimalphabete kombinieren, um die Sicherheit des Chiffrats zu erhöhen.
Bezogen auf das weiter oben vorgestellte Verschiebechiffre würde das bedeuten, daß jeder Buchstabe nicht um denselben, festen Wert im Alphabet verschoben wird, sondern durch eine Anzahl, die durch irgendeine alternierende Vorschrift erzeugt wird. Zum Beispiel könnte der erste Buchstabe um eine Stelle verschoben werden, der zweite um zwei, der dritte um drei, und so weiter.
Tabula Recta
Die Tabula Recta, die vom Benediktinerabt Johannes Trithemius (1462-1516), der die ersten gedruckten Bücher über Kryptographie verfasste, erdacht wurde, vewendet, ähnlich wie das Polybios-Chiffre, eine Matrix. Allerdings enthält hier jede der 24 Zeilen alle Buchstaben des Alphabets (im Falle der Tabula Recta ebenfalls 24, da es im Lateinischen kein J und kein U gibt). Der Unterschied zwischen den Zeilen besteht lediglich darin, daß das Alphabet jeweils später beginnt (und die ausgelassenen Buchstaben später hinten angehängt werden, um die Zeile zu komplettieren). Er selber schreibt6 dazu:
»In dieser regelmäßigen oder viereckigen Tabelle von Buchstaben findet man durch Veränderung („per mutationem“) oder Umsetzung („transpositionem“) das gebräuchliche Alphabet unserer lateinischen Buchstaben, die in ihrer Gesamtheit Monogramme (einzelne Buchstaben) darstellen, nämlich 24 mal 24, das ergibt die Zahl von 576 und multipliziert man diese mit genauso vielen (24), ergibt sich ein wenig weniger als 14.000.«
Die Idee lag nun darin, den ersten Buchstaben des Klartextes mit der ersten Zeile zu verschlüsseln und den zweiten mit der zweiten (vgl. oben angedeutetes Verfahren des Polyalphabets beim Verschiebechiffre). Diese Vorgehensweise selber bezeichnet man als progressive, also voranschreitende, Chiffrierung und kommt in späteren Kapiteln der Geschichte und dieser Ausarbeitung noch mehrfach vor.
Vigenere-Verschlüsselung
Mit der Vignére Verschlüsselung, benannt nach dem Diplomaten Blaise de Vigenère (16. Jahrhundert), tauchte das Prinzip eines Passworts zum ersten Mal auf. Dieses geheime Wort wurde so interpretiert, daß die Position seiner Zeichen jeweils die Verschiebung des Alphabets für das entsprechende Zeichen des Klartext ergab7.
Nehmen wir als zu verschlüsselnden Klartext erneut "IT Sicherheit" an. Passwort soll sein "passwort". In diesem Falle würde das Alphabet um 16 Stellen verschoben werden (da "P" der 16. Buchstabe im Alphabet ist). Das I (Buchstabe Nr. 9 im Alphabet) von "IT Sicherheit" müßte demnach um 16 Stellen auf Position 25 (also ein Y) verschoben werden. Analog würde es mit dem zweiten Buchstaben "T" des Klartextes geschehen, der gemäß des zweiten Buchstabens des Passworts "A" um eine Stelle verschoben werden müßte (U).
Ist das Passwort abgearbeitet, aber der Klartext noch nicht, so hängt man es einfach erneut an, so daß im Sinne des polyalphabetischen Verfahrens das erste Alphabet das normale ist und das zweite eine Reihenfolge von Buchstaben, die dieselbe Länge hat, wie der Klartext und in unserem Beispiel so aussehen würde: »passwortpasswortpasswortpasswortpasswortpas....«
Vernam Verschlüsselung
Die Vernam Verschlüsselung, benannt nach ihrem Erdenker, dem amerikanischen Kryptologen Gilbert Vernam (1890-1960), benutzt dasselbe Prinzip wie die Vignére-Verschlüsselung. Allerdings ist das Passwort genauso lang wie der Klartext8 und wird nach einmaliger Verwendung nicht mehr benutzt. Unter der Voraussetzung, daß es gewissenhaft angewendet wird und das Einmalpasswort (One Time Pad) tatsächlich aus zufälligen Zeichen besteht, gilt dieses Verfahren als informationstheoretisch sicher und kann nachweislich nicht gebrochen werden.
Zwar erfüllt dieses Verfahren den Anspruch darauf, daß sich die Sicherheit eines Verfahrens nicht auf die Geheimhaltung des Systems (Obscurity) aufbauen darf, sondern einzig durch die Geheimhaltung des Schlüssels, allerdings muß bedacht werden, daß es wohl keinen praktischen Unterschied macht, ob man einen Text mit 100 Zeichen vor fremdem Zugriff schützen muß, oder einen Schlüssel, der ebenfalls 100 Zeichen Länge hat.
Sicherheit Polyalphabetischer Chiffren
Wie auch die monoalphabetischen Verfahren, bietet der polyalphabetische Ansatz - sehen wir von der Vernam Verschlüsselung mir ihren ganz eigenen Nachteilen ab - keinen ausreichenden Schutz und kann gebrochen werden. Wenn zum Beispiel die Schlüssellänge bekannt ist, so kann man alle Zeichen des Chiffrats, die diesen Abstand haben, mit dem selben Verschiebechiffre substituieren.
Der Kasiski-Test, benannt nach dem preußischen Infanteriemajor Friedrich Wilhelm Kasiski (1805 - 1881), soll diese Schlüssellänge ermitteln und macht sich dabei zunutze, daß es durchaus vorkommt, daß Wiederholungen im Klartext (vor allem Silben) mit Wiederholungen des Schlüssels aufeinanderfallen. Diese Abstände zwischen den Vorkommnissen müssen demnach wahrscheinlich vielfache der Schlüssellänge oder die Schlüssellänge selber sein. Danach bedarf es nur noch einer Häufigkeitsanalyse.
Wie auch schon beim monoalphabetischen Ansatz, ist eine Häufigkeitsanalyse der Buchstaben, die in der zu entschlüsselnden Sprache vorkommen, ein wunder Punkt des Verfahrens. Jeder Kreuzworträtselfan weiß, daß in der deutschen Sprache vor allem E's und N's häufiger vorkommen, als andere Buchstaben. Siehe dazu die folgende Graphik8, die das Vorkommen der verschiedenen Zeichen in der deutschen Sprache statistisch aufzeigt:
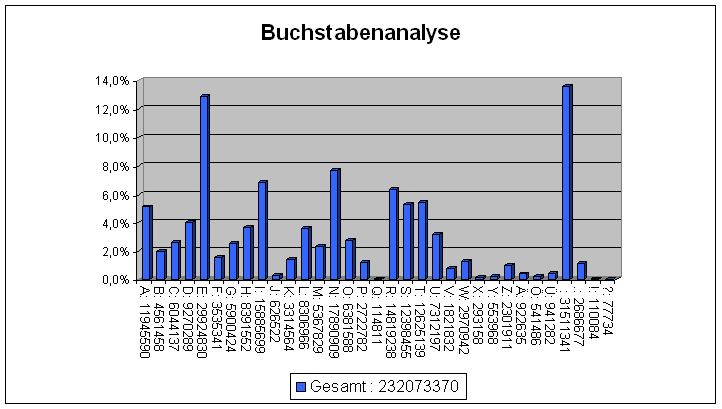
Abbildung 1: Häufigkeit der Buchstaben in deutscher Prosa.
Vor allem längere Texte nähern sich recht gut dieser Statistik an. Bei kürzeren Texten jedoch besteht die Gefahr, daß sie aus verschiedenen, vorhersagbaren Phrasen oder Textfragmenten bestehen müssen, die den Mindestinformationsgehalt darstellen, den es zu kommunizieren gilt.
Somit ist das eine wie das andere der Gefahr der unauthorisierten Entschlüsselung ausgesetzt und die polyalphabetischen Substitutionschiffren können nicht als sicher betrachtet werden (Ausnahme: Vernam).
voriges Kapitel | nächstes Kapitel



